บทที่ 2 ทศนิยม

บทที่2

                         เรื่อง ทศนิยม

ทศนิยมนั้นจะเข้ามามีบทบาทในชีวิตประจำวันของเราตลอด ไม่ว่าจะเป็นการบอกค่าของเงินที่เราใช้การบอกเวลา บอกหน่วยความยาว ฯลฯ

          ทศนิยม หมายถึง ค่าของจำนวนเต็มที่แบ่งออกเป็นสิบส่วน ร้อยส่วน พันส่วน .... เท่า ๆ กัน ซึ่งเขียนได้ในรูปของเศษส่วน

การอ่านทศนิยม

เลขที่อยู่หน้าทศนิยมเป็นเลขจำนวนเต็ม อ่านเช่นเดียวกับตัวเลขจำนวนเต็มทั่วไป ส่วนตัวเลขหลังจุดทศนิยมเป็นเลขเศษของเศษส่วนซึ่งมีค่าไม่ถึงหนึ่ง อ่านตามลำดับตัวเลขไป เช่น 635.1489 อ่านว่า หกร้อยสามสิบห้าจุดหนึ่งสี่แปดเก้าถ้าเลขจำนวนนั้นไม่มีจำนวนเต็ม จะเขียน 0 (ศูนย์) ไว้ตำแหน่งหลักหน่วยหน้าจุดได้ เช่น .25เขียนเป็น 0.25 ก็ได้

                                                        

                                                         การเรียกตำแหน่งทศนิยม

                                                                                      

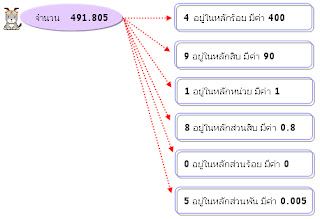
การกระจายทศนิยมจำนวน 327.35 จะเขียนให้อยู่ในรูปกระจายได้ดังนี้
3 อยู่ในหลักร้อย มีค่า 300

2 อยู่ในหลักสิบ มีค่า 20

7 อยู่ในหลักหน่วย มีค่า 7

3 อยู่หลังจุดเป็นตัวแรกเรียกว่าหลักส่วนสิบ ซึ่งมีค่า หรือ 0.3

5 อยู่หลังจุดเป็นตัวที่สองเรียกว่าหลักส่วนร้อย ซึ่งมีค่า หรือ 0.05

ดังนั้น 327.35 อ่านว่า สามร้อยยี่สิบเจ็ดจุดสามห้าหรือสามารถเขียนในรูปกระจายการบวกได้คือ 327.35 = 300 + 20 + 7 + 0.3 + 0.05

จำนวนตรงข้ามของทศนิยม

            ทศนิยมที่เป็นบวกและทศนิยมที่เป็นลบที่มค่าสัมบูรณ์เท่ากัน จะอยู่คนละข้างของ 0 และอยู่ห่างจาก 0 เป็นระยะเท่ากัน เช่น -1.5 และ 1.5

·                     -1.5 เป็นจำนวนตรงข้ามของ 1.5 และ 1.5 เป็นจำนวนตรงข้ามของ -1.5 ,

·                     -1.75 เป็นจำนวนตรงข้ามของ 1.75 และ 1.75 เป็นจำนวนตรงข้ามของ -1.75

·                     ถ้า a เป็นทศนิยมใด ๆ จำนวนตรงข้ามของ a มีเพียงจำนวนเดียวเขียนแทนด้วย -a และ a + ( - a ) = ( - a ) + a = 0 

• จำนวนตรงข้ามของ -1.75 เขียนแทนด้วย - ( - 1.75 )
  จำนวนตรงข้ามของ -1.75 คือ 1.75 เนื่องจากจำนวนตรงข้ามของ -1.75 มีเพียงจำนวนเดียว ดังนั้น -( -1.75 ) = 1.7
  ถ้า a เป็นทศนิยมใด ๆ จำนวนตรงข้ามของ - a คือ a และเขียนแทนด้วย -( -a )
  ในการหาผลลบของทศนิยมใด ๆ ใช้ข้อตกลงเดียวกันที่ใช้ในการหาผลลบของจำนวนเต็ม คือ

ตัวตั้ง - ตัวลบ = ตัวตั้ง + จำนวนตรงข้ามของตัวลบ
เมื่อ a และ b แทนทศนิยมใด ๆ a - b = a+จำนวนตรงข้ามของ b หรือ a - b = a +( - b ) เช่น 5.01 - 2.32 = 5.01 + (-2.32) , ( -4.17 ) -1.32 = ( -4.17 ) + ( -1.32 )

การบวกเลขทศนิยม

                  คือ ตั้งให้จุดทศนิยมตรงกัน แล้วทำการบวกตามการบวกเลขธรรมดาทั่ว ๆ ไป เช่น

35.05 , 27.09 35.05 + 27.09 62.14

การลบทศนิยม

·                     จงหาผลลบ 63.02 - ( -86.38 )
วิธีทำ 63.02 - ( -86.38 ) = 63.02 + ( 86.38 )
63.02
+
86.38
149.40 ดังนั้น 63.02 - ( -86.38 ) = 149.40

·                     จงหาผลลบ ( - 125.17 ) - ( - 72.9 )
วิธีทำ ( -125.17 ) - (-72.9 ) = ( -125.17 ) + 72.90
-125.17
+
72.90
-52.27 ดังนั้น ( -125.17 ) - ( -72.9 ) = - 52.27

·          การหาผลคูณโดยใช้การบวกทศนิยมซ้ำ ๆ กัน

·          

·                     การคูณทศนิยมด้วยจำนวนนับ อาจใช้วิธีเปลี่ยนการคูณให้อยู่ในรูปของการบวกทศนิยมนั้นหลาย ๆ ครั้ง โดยจำนวนของทศนิยมที่นำมาบวกกันเท่ากับจำนวนนับนั้นแล้วใช้หลักการบวกทศนิยม จะสังเกตได้ว่า การคูณนั้นก็เหมือนกับการนำเอาทศนิยมจำนวน ๆ หนึ่ง มาบวกกันให้เท่ากับจำนวนที่เราต้องการ เช่น

·         เราต้องการ หา 4 เท่าของ 0.4 

·         0.4 * 4 = 0.4 + 0.4 + 0.4 + 0.4  = 1.6

·          

·                      จะเห็นว่าได้ผลลัพธ์เท่ากัน ดังนั้นก็สามารถบอกได้ว่า การหาผลคูณโดยใช้วิธีการนำทศนิยมมาบวกซ้ำ ๆ กัน ให้เท่ากับจำนวนที่เอามาคูณได้ และอาจใช้วิธีตั้งหลักเลขและจุดทศนิยมให้ตรงกัน แล้วบวกกันโดยใช้หลักการเช่นเดียวกับการบวกจำนวนนับ

ทศนิยม และเศษส่วน
                                              
                                              
6.1 การเขียนทศนิยมให้เป็นเศษส่วน
ตัวอย่าง จงเขียน 2.5 ให้เป็นเศษส่วน
วิธีทำ 2.5 = 2 กับ 5 ใน 10

6.2 การเขียนเศษส่วนให้เป็นทศนิยม
1.) เศษส่วนที่มีส่วนเป็น 10 หรือ 100 หรือ 10 ยกกำลัง สามารถเปลี่ยนเป็นทศนิยมได้เลย เช่น 75/100 = 0.75
2.) เศษส่วนที่ไม่มีส่วนเป็น 10 หรือ 100 หรือ 10 ยกกำลัง ให้เปลี่ยนเป็นเศษส่วนที่มีส่วนเป็น 10 หรือ100 หรือ 10 ยกกำลังก่อน เช่น
6.1 การเขียนทศนิยมให้เป็นเศษส่วน
ตัวอย่าง จงเขียน 2.5 ให้เป็นเศษส่วน
วิธีทำ 2.5 = 2 กับ 5 ใน 10

6.2 การเขียนเศษส่วนให้เป็นทศนิยม
1.) เศษส่วนที่มีส่วนเป็น 10 หรือ 100 หรือ 10 ยกกำลัง สามารถเปลี่ยนเป็นทศนิยมได้เลย เช่น 75/100 = 0.75
2.) เศษส่วนที่ไม่มีส่วนเป็น 10 หรือ 100 หรือ 10 ยกกำลัง ให้เปลี่ยนเป็นเศษส่วนที่มีส่วนเป็น 10 หรือ100 หรือ 10 ยกกำลังก่อน เช่น

              

        17

= - 52.27

 การหาผลคูณโดยใช้การบวกทศนิยมซ้ำ ๆ กัน

            การคูณทศนิยมด้วยจำนวนนับ อาจใช้วิธีเปลี่ยนการคูณให้อยู่ในรูปของการบวกทศนิยมนั้นหลาย ๆ ครั้ง โดยจำนวนของทศนิยมที่นำมาบวกกันเท่ากับจำนวนนับนั้นแล้วใช้หลักการบวกทศนิยม จะสังเกตได้ว่า การคูณนั้นก็เหมือนกับการนำเอาทศนิยมจำนวน ๆ หนึ่ง มาบวกกันให้เท่ากับจำนวนที่เราต้องการ เช่น

ซ้ำ ๆ กัน ให้เท่ากับจำนวนที่เอามาคูณได้ และอาจใช้วิธีตั้งหลักเลขและจุดทศนิยมให้ตรงกัน แล้วบวกกันโดยใช้หลักการเช่นเดียวกับการบวกจำนวนนับ

                                              ทศนิยม และเศษส่วน

6.1 การเขียนทศนิยมให้เป็นเศษส่วน

ตัวอย่าง จงเขียน 2.5 ให้เป็นเศษส่วน

วิธีทำ 2.5 = 2 กับ 5 ใน 10

6.2 การเขียนเศษส่วนให้เป็นทศนิยม

1.) เศษส่วนที่มีส่วนเป็น 10 หรือ 100 หรือ 10 ยกกำลัง สามารถเปลี่ยนเป็นทศนิยมได้เลย เช่น 75/100 = 0.75

2.) เศษส่วนที่ไม่มีส่วนเป็น 10 หรือ 100 หรือ 10 ยกกำลัง ให้เปลี่ยนเป็นเศษส่วนที่มีส่วนเป็น 10 หรือ 100 หรือ 10 ยกกำลังก่อน เช่น

                                    เรียนรู้เพิ่มเติม การเขียนเศษส่วนเป็นทศนิยม

การกระจายทศนิยมจำนวน 327.35 จะเขียนให้อยู่ในรูปกระจายได้ดังนี้
3 อยู่ในหลักร้อย มีค่า 300

2 อยู่ในหลักสิบ มีค่า 20

7 อยู่ในหลักหน่วย มีค่า 7

3 อยู่หลังจุดเป็นตัวแรกเรียกว่าหลักส่วนสิบ ซึ่งมีค่า หรือ 0.3

5 อยู่หลังจุดเป็นตัวที่สองเรียกว่าหลักส่วนร้อย ซึ่งมีค่า หรือ 0.05

ดังนั้น 327.35 อ่านว่า สามร้อยยี่สิบเจ็ดจุดสามห้าหรือสามารถเขียนในรูปกระจายการบวกได้คือ 327.35 = 300 + 20 + 7 + 0.3 + 0.05